The Math Behind GPS: How Your Phone Knows Where You Are
In today’s hyper-connected world, the Global Positioning System (GPS) has become a staple technology in our lives. Whether you’re navigating through traffic, tracking a lost phone, or monitoring global logistics, GPS powers countless applications with incredible precision. But behind the seamless experience lies an intricate tapestry of mathematics, physics, and engineering, carefully orchestrated to pinpoint your exact location.
This article takes a deep dive into the science and technology that make GPS possible. From the fundamental geometry of trilateration to the challenges of relativity, satellite constellations, and atmospheric effects, you’ll discover how this revolutionary system works in harmony to determine your position within mere meters.

What Is GPS, and How Does It Work?
GPS, or the Global Positioning System, is a satellite-based navigation system operated by the United States government. While initially developed for military purposes in the 1970s, GPS became accessible to civilians in the 1980s, evolving into an essential tool for everything from personal navigation to scientific research.
The Basics of GPS
At its core, GPS operates by:
- Using a constellation of satellites that orbit the Earth, continuously broadcasting signals.
- Measuring distances from these satellites to a receiver, such as your smartphone.
- Applying mathematical methods, particularly trilateration, to determine the receiver’s location.
- Refining the calculations through error correction techniques, accounting for clock discrepancies, relativistic effects, and atmospheric distortions.
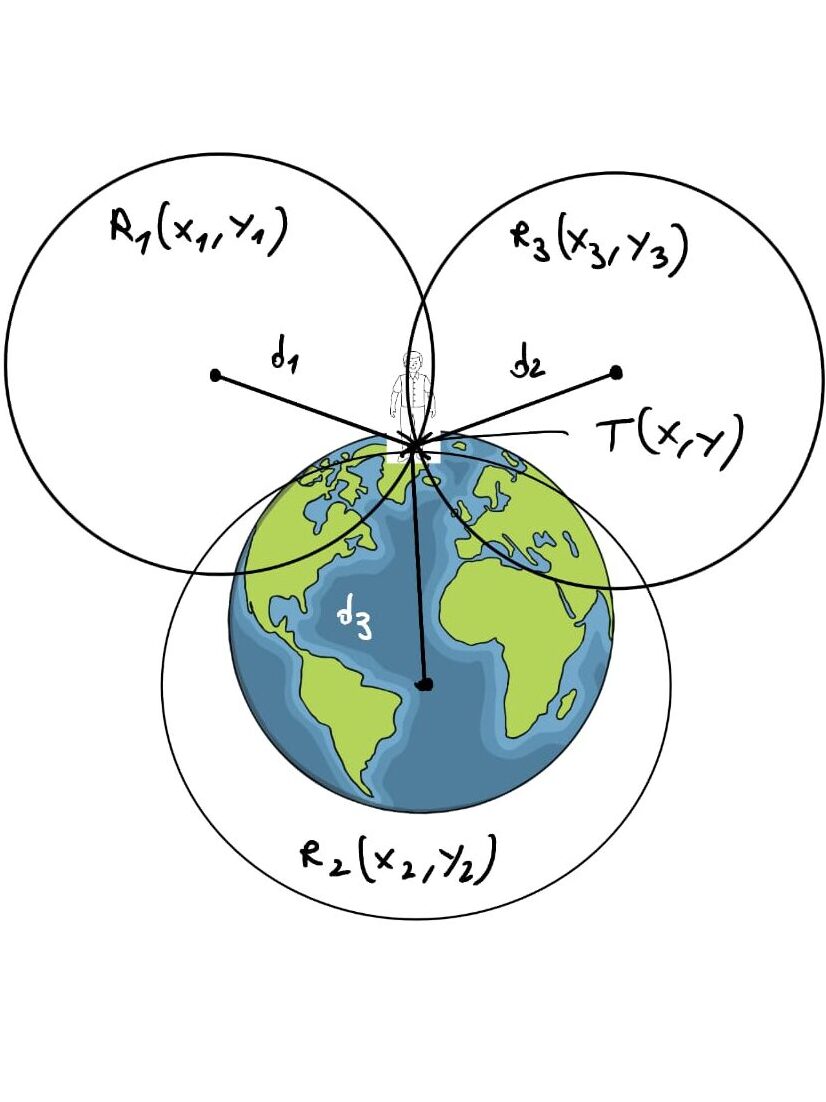
1. Trilateration: The Core Principle Behind GPS
The concept of trilateration lies at the heart of GPS. Trilateration is a mathematical method used to find an unknown location by measuring its distance from multiple known reference points. Unlike triangulation, which uses angles, trilateration relies solely on distances.
How Trilateration Works
Imagine you are standing in a park with three radio towers around you. If you know your exact distance from each tower:
- You are 5 kilometers from Tower A.
- You are 7 kilometers from Tower B.
- You are 3 kilometers from Tower C.
If you draw a circle around each tower with a radius equal to your distance from it, the three circles will intersect at a single point – your exact location.
Applying Trilateration in GPS
In GPS, satellites act as these reference points, and their positions in space are precisely known. The receiver calculates its distance to each satellite by measuring the time it takes for a signal to travel from the satellite to the receiver. By solving multiple equations for distances to at least four satellites, the receiver determines its position in three-dimensional space.
The mathematical formula for the distance between a satellite and a receiver is: d = sqrt{(x – x_1)^2 + (y – y_1)^2 + (z – z_1)^2}
Where:
- x_1, y_1, z_1 are the satellite’s coordinates,
- x, y, z are the unknown coordinates of the receiver,
- d is the measured distance.
This method of solving simultaneous equations forms the foundation of GPS positioning.
2. The Role of Coordinate Systems in GPS
For trilateration to work, both the satellites and the receiver must operate within a common coordinate system that accurately models the Earth’s shape.
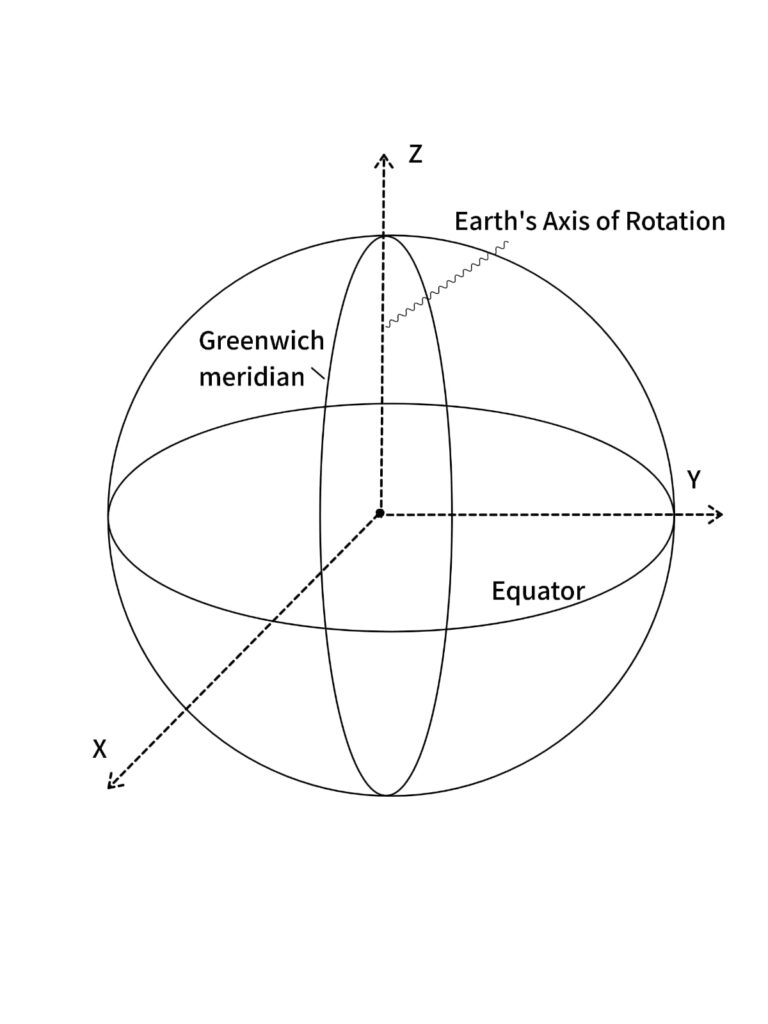
Earth-Centered, Earth-Fixed (ECEF) Coordinate System
The GPS system uses the ECEF coordinate system, a 3D Cartesian coordinate system:
- The origin is the Earth’s center of mass.
- The X-axis points toward the intersection of the equator and the prime meridian.
- The Y-axis points eastward along the equatorial plane.
- The Z-axis points toward the North Pole.
This system accounts for the Earth’s rotation and slightly ellipsoidal shape (flattened at the poles and bulging at the equator).
From Cartesian to Latitude and Longitude
While GPS calculations are performed in Cartesian coordinates (x,y,z)(x, y, z), the results are often converted into latitude, longitude, and altitude for practical use. This transformation involves solving equations that take into account the Earth’s ellipsoid model, such as the World Geodetic System 1984 (WGS84).
3. The Satellite Constellation: A Global Network
The GPS constellation consists of at least 24 active satellites, along with additional spares, ensuring reliable global coverage.
Key Facts About GPS Satellites
- Altitude: Satellites orbit at approximately 20,200 kilometers above the Earth.
- Orbital Period: Each satellite completes an orbit in about 12 hours.
- Orbital Planes: The satellites are arranged in six orbital planes, each containing four satellites, strategically positioned to ensure that at least four satellites are visible from any point on Earth.
Why Multiple Satellites Are Necessary
- Global Coverage: A minimum of 24 satellites ensures continuous global availability.
- Redundancy: Extra satellites provide backup in case of maintenance or failure.
- Accuracy: More satellites improve position calculations by reducing uncertainty.
Each satellite continuously broadcasts:
- Its position in space,
- The time the signal was transmitted,
- Health and status data.

4. Measuring Distance: The Core Calculation
GPS calculates distances by measuring the time delay of signals sent from satellites to the receiver. Since radio signals travel at the speed of light (c=3×10_8 m/s), the distance d is calculated as: d=c⋅t
Where:
- t is the time it takes for the signal to travel,
- c is the speed of light.
Atomic Clocks: The Heart of Precision
GPS satellites are equipped with atomic clocks, which provide unparalleled accuracy in timekeeping. These clocks are accurate to within nanoseconds, ensuring that the time data embedded in the signals is reliable.
Synchronization of Clocks
While satellite clocks are incredibly accurate, the clocks in GPS receivers are less precise. This discrepancy is corrected by using a fourth satellite, which provides additional data to resolve timing errors.

5. The Effects of Relativity on GPS
Einstein’s theory of relativity has a profound impact on GPS accuracy. Both special relativity and general relativity come into play.
Special Relativity
Satellites move at high speeds (~14,000 km/h). According to special relativity, time on a moving clock runs slower compared to a stationary clock. This causes satellite clocks to lose about 7 microseconds per day relative to Earth-based clocks.
General Relativity
Satellites orbit in weaker gravitational fields than clocks on Earth. General relativity predicts that clocks in weaker gravity run faster. This effect causes satellite clocks to gain about 45 microseconds per day.
Net Effect
Combining these effects, satellite clocks run approximately 38 microseconds faster per day than Earth clocks. While this seems negligible, if left uncorrected, it would result in positional errors of up to 10 kilometers per day. GPS systems account for these relativistic effects to maintain accuracy.
6. Atmospheric Effects on GPS Signals
As signals travel through the atmosphere, they are subject to distortions caused by:
- The ionosphere: Charged particles in this layer slow down radio signals.
- The troposphere: Water vapor and temperature variations introduce additional delays.
Mitigating Atmospheric Errors
- Dual-frequency GPS receivers: These devices compare signals sent on two different frequencies to estimate and correct ionospheric delays.
- Empirical models: Tropospheric delays are corrected using data from weather stations.
7. Refining Accuracy: Least Squares and Error Minimization
After an initial position is estimated, GPS receivers use the least squares method to minimize errors and refine the result. This iterative process reduces residuals—the differences between observed and calculated distances.
How Least Squares Works
- An approximate position is calculated using trilateration.
- The algorithm adjusts this position by minimizing discrepancies.
- The process repeats until the most accurate position is determined.

Conclusion: The Genius of GPS
The Global Positioning System is a masterpiece of scientific innovation, seamlessly blending mathematics, physics, and engineering to deliver precise positioning capabilities. From the geometry of trilateration to the complexities of relativity and atmospheric corrections, GPS represents the pinnacle of human ingenuity.
Next time you use your phone to navigate, remember the incredible science and technology working behind the scenes to guide you – proof that mathematics truly powers the modern world.







